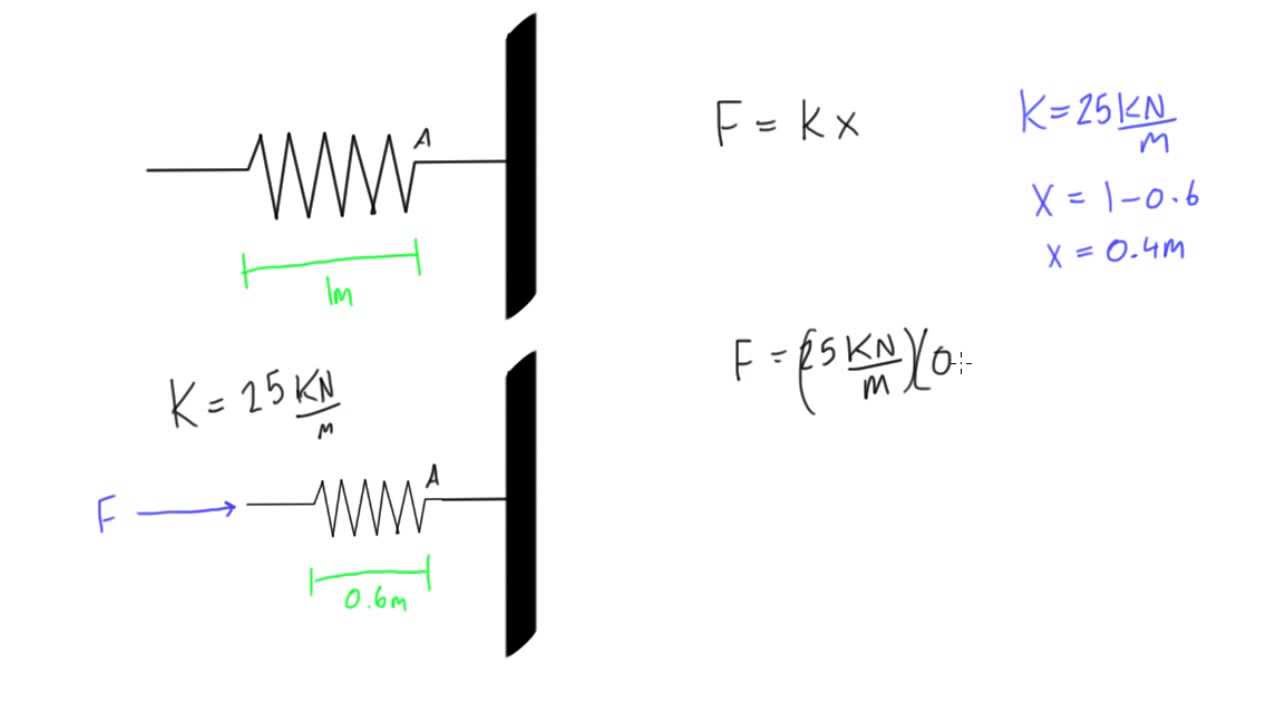
When the spring is stretched by an external force, the work done by the spring, w = 1 2 k x 2. Plug in the given values for the distance.
Equation For Work Done On A Spring. $$ pe_{spring} = \frac{1}{2}k(\delta x)^2 $$ if i understand the question correctly, your $\delta x$ is the 30 centimeters, or 0.3 meters. Where x is the distance from the equilibrium point of the spring.
Ch 3 energy transfer by work, heat and mass From slideshare.net
W = 1/2 k ⋅ x 2. Now, when the spring releases, the initial position is x2 while the final position is x1, thus the order of. The displacement of the spring from its position at equilibrium is x, the spring constant is k.
Ch 3 energy transfer by work, heat and mass
The force exerted by the spring on the body which deforms it:: The force is defined to be linearly increasing with the distance, x: Work done on elastic springs, and hooke�s law. The constant k is called the spring constant and is a measure of the stiffness of the spring.
Source: youtube.com
Work done = force × distance. W = ∫ x 1 x 2 − k x ⋅ d x = 1 2 k x 1 2 − 1 2 k x 2 2. Put the two values of stretched lengths given in the problem for the same values of force and force constant. The work done on the spring is.
Source: youtube.com
F=kx where k is the spring constant. If we continued to apply that force of n newtons to move the mass some distance, d meters, then he work done would be w = n*d joules. The formula for the work to stretch or compress a spring is: W = 1/2 k ⋅ x 2. The constant k is called the.
Source: hockeyschtick.blogspot.com
A spring is stretched 60 cm, and it takes a force of 40 newtons to hold it there. Work done (w) is measured in joules (j) force (f) is measured in newtons (n) distance moved along the line of action of the force (s) is. W = ∫ a b f ( x) d x w=\int^b_af (x)\ dx w =.
Source: youtube.com
The force exerted by the spring on the body which deforms it:: Plugging the first equation into the second yeilds: The formula for work done by a spring is: The force is defined to be linearly increasing with the distance, x: Where w w w is the work done, f ( x) f (x) f ( x) is the force.
Source: slideshare.net
Now, when the spring releases, the initial position is x2 while the final position is x1, thus the order of. F = k⋅ x f = k ⋅ x. Two equations for a spring are (variables defined below): Plug in the given values for the distance and spring constant to solve for the potential energy. The displacement x is measured.
Source: slideserve.com
The resultant potential energy will be positive as, when released, the displacement will be along the positive horizontal axis. W = ∫ x 1 x 2 f ⋅ d x. The equation for spring potential energy is. W = (1 / 2) k x 2. Let�s start with the derivation of the above equation.
Source: slideshare.net
W = ∫ x 1 x 2 f ⋅ d x. The answers to your questions: Elastic potential energy = 0.5 × spring constant × (extension) 2 [e_e = \frac{1}{2}~k~e^2] Work done on an elastic spring during compression or extension from rest, is known as the elastic potential energy. The work required to stretch or compress a spring.
