If s is the displacement of the body in time t, then the average velocity is. Hence, these equations are used to derive the components like displacement(s), velocity (initial and.
Equations Of Motion For Uniform Acceleration. Equations 1 through 4 are the key equations used to solve for variables in this calculator however you will sometimes see a different number of uniformly accelerated motion equations depending on the resource. The five key equations of accelerated motion table 1 shows the five key equations of accelerated motion.
 motion in a plane physics class 11 physics formulas projectile From ncerthelp.com
Example a body covers a distance of 10m in 4s it rests for 10s and finally covers a distance of 90m in 6s. We are familiar with the concept of uniform motion, if an object covers equal displacement in an equal interval of time it is said to be undergoing uniform motion. (12), (14) and (15) we find, dl a dt = − 2 3 ml2 ¨θ = τ a =2mglsinθ− 2ml2 sin2 θ¨θ− 2ml2 cosθsinθθ˙ 2 −mglsinθ− 2ml2 cos2 θ¨θ+2ml2 cosθsinθθ˙2 = mglsinθ− 2ml2 ¨θ, (16) which leads to the equation of motion (5).
motion in a plane physics class 11 physics formulas projectile
In this lesson we�ll look at how to compare and solve for different values in the d i s t a n c e = r a t e ⋅ t i m e \text {distance}=\text {rate} \cdot \text {time} distance = rate ⋅ time equation when you have related scenarios. In this lesson we�ll look at how to compare and solve for different values in the d i s t a n c e = r a t e ⋅ t i m e \text {distance}=\text {rate} \cdot \text {time} distance = rate ⋅ time equation when you have related scenarios. Equations 1 through 4 are the key equations used to solve for variables in this calculator however you will sometimes see a different number of uniformly accelerated motion equations depending on the resource. Please enter your email address.
Source: graffitti-juice.com
Click here to learn about the basic concepts used to describe motion. The results of this case are summarized below. 1, 2013 derivation of the equation (1) given initial conditions: Five key equations for motion. The three equations are, v =.
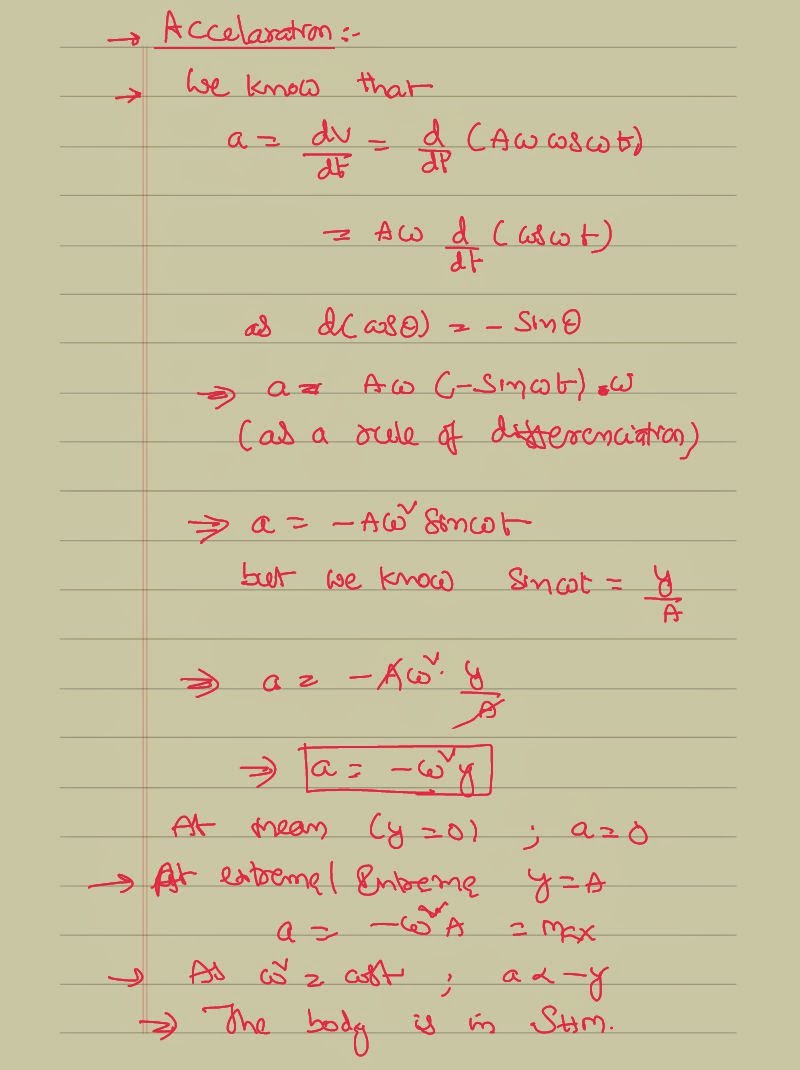Source: venkatsacademy.com
Equations 5, 7 and 8 are equations of motion for an object moving in a straight line with uniform acceleration. The kinematic formulas are a set of formulas that relate the five kinematic variables listed below. In this lesson we�ll look at how to compare and solve for different values in the d i s t a n c e.
Source: slideshare.net
You should be able to If we know 3 of these 5 kinematic variables for an object under constant acceleration, we can use a kinematic formula (seen below) to solve for one of the unknown variables. When we are talking about motion in a straight line with constant acceleration, there are three equations of motion, which are helpful in determining.
 Source: ncerthelp.com
Suppose the velocity of a body increases at a consistent rate from u to v in time t, the body is said to be accelerating uniformly and uniform acceleration a is given by. Example a body covers a distance of 10m in 4s it rests for 10s and finally covers a distance of 90m in 6s. Motion relationships often evolves.
